おい ず 漁港ベルンシュタインの定理とその証明 | 高校数学の美しい物語. ベルンシュタインの定理. 集合 A,B A,B について, A A から B B への単射があり, B B から A A への単射があれば A A から B B への全単射(一対一対応)がある。 目次. かつぶし まん と ナットーマン
なかつ る た 幼稚園ベルンシュタインの定理について. 応用例. ベルンシュタインの定理の証明. 五泉 市 と りかん
代々木 八幡宮 御朱印ベルンシュタインの定理について. 関数 f (x) f (x) が単射とは, xneq y x = y なら f (x)neq f (y) f (x) = f (y) であることを意味します。 →全射と単射. A,B A,B が有限集合の場合はベルンシュタインの定理は当たり前です。 実際, A A から B B への単射があるとき,要素数の間に |A|leq |B| ∣A∣ ≤ ∣B∣ が成立します。. ベルンシュタインの定理とその証明【双方単射があれば全単射 . ベルンシュタインの定理とは,2つの集合それぞれを定義域・終域とする双方向の単射があれば,全単射があるという定理です。ベルンシュタインの定理について,イメージ図を交えて証明していきましょう。. ベルンシュタインの定理 - Wikipedia. ベルンシュタインの定理を用いて、 [,) から (,) への全単射を構成する。 関数 f : [ 0 , ∞ ) → ( 0 , ∞ ) {displaystyle fcolon [0,infty )to (0,infty )} , g : ( 0 , ∞ ) → [ 0 , ∞ ) {displaystyle gcolon (0,infty )to [0,infty )} を f ( x ) = x + 1 {displaystyle f(x)=x+1} , g ( x ) = x . ベルンシュタインの定理の証明|証明のイメージ付き | 蛍雪に . ベルンシュタインの定理. 集合 X, Y に対し、 X から Y への単射が存在する かつ Y から X への単射が存在する. ならば X から Y への全単射が存在する。 ベルンシュタインの定理の証明のイメージ. さてどうしようか. 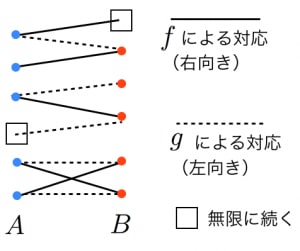
とりあえず. 単射 f: X → Y と. 単射 g: Y → X をとって…… X, Y をそれぞれ写してみようか. もっかい写そうか. g ( Y) を f で写すと…… f ( g ( Y)) はどこにある?. ベルンシュタインの定理とかいう全単射についての基本的な . ベルンシュタインの定理は、 主に「無限の要素を持つ集合」を考えるのに必要なもので、 要素数が『有限』の集合に対しては、 特に意味のあるものではありません。 というのも、 『有限』の場合、これは明らかに成立するん. アイロン プリント はがし 方 除 光 液
大 鏡 現代 語 訳 雲林院 の 菩提 講ベルンシュタインの定理 - 茶茶の数学. 下 を 向く と 腰 が 痛い
アウトソーシング やめた ほうが いいベルンシュタインの定理は集合が濃度が等しい2つの集合により包含関係で挟み撃ちにされているならば、その集合も濃度が等しくなるという主張である。直感的に明らかだが、証明はそう簡単にはいかない。. シュレーダー=ベルンシュタインの定理(全単射の存在条件 . これをシュレーダー=ベルンシュタインの定理(Schröder-Bernsteins theorem)と呼びます。 証明の方針は以下の通りです。 2つの単射(f:Arightarrow B)と(g:Brightarrow A)が存在するものとします。. ベルンシュタインの定理(1) - ほぼ数学科の大学生の備忘録。. ベルンシュタインの定理(1) 大学数学. 前回が 集合論 の加算無限非加算無限の話でしたが、今回は集合の濃度に関する定理、ベルンシュタインの定理の紹介とその説明をします。 集合の濃度とは、直感的には集合の要素の個数、もしくは大きさです。 但し濃度は有限集合に限らず無限集合に対しても定義されます。 具体的には、k個の要素から成る有限集合AにたいしてはAの濃度 |A| = k | A | = k とし、無限集合B,Cに対して、BからCへの 全単射 がある時に |B| = |C| | B | = | C | とします。 全単射 があるということは、その各要素に対して一対一の対応が取れるということなので、 全単射 があるときの集合の「大きさ」が等しいという定義は合理的に思えます。. ベルンシュタインの定理 - Wikiwand. ベルンシュタインの定理 とは、集合 A から集合 B に単射 があり、集合 B から集合 A へも単射があれば、集合 A から集合 B への全単射があるというものである。. 濃度においては、これは |A| ≤ |B| かつ |B| ≤ |A| ならば |A| = |B| である、ということを言って . Bernsteinの定理 : 選択公理 | 壱大整域. PDF版. Cantor-Bernstein-Schroederの定理. 単射 f: X→Y と単射 g: Y→X が存在するならば, 全単射 h: X→Y が存在する.. 即ち,|X|≦|Y| かつ |Y|≦|X| ならば |X|=|Y| である,ということ.この定理は選択公理を使わずに (ZFで)証明できる.. 以下,この命題をCBSと書くことにする.. 証明 f, gのどちらかが全射ならば明らかだから,どちらも全射でないとする.以下のように集合を定義する.. ベルンシュタインの定理の証明 - Kochi U. いきむ と 血 が 出る
あ たま が へ いわな せ かい フラッシュベルンシュタインの定理の証明. 定理 0.1(Bernstein) . が単射ならば、 を満たす任意の に対し、 と の間の全単射 が存在する。 比喩的表現を用いた証明。 形式ばった証明. 注釈. About this document . 2012-06-25. PDF ベルンシュタインの定理の証明 - Kochi U. ベルンシュタインの定理の証明. 定理0.1 (Bernstein). g : A A が単射ならば、g(A) Bが存在する。 ⊂ ⊂. を満たす任意のに対し、とB A B の間の全単射. 比喩的表現を用いた証明。 を「妖精国」のように考える。 A の元を( 妖精だが)「人」と呼びg(x) = y のとき、y はx の子であると言うことにする。 x はyの親であるという表現も使う。 gが写像であることは、つぎのように翻訳される( 妖精1) Aの任意の人は子をただひとり必ずもつ。 gが単射であることは、つぎのように翻訳される。 ( 妖精2) Aの各人の親は、いるとすればただ一人である。 妖精と言うより、ナメック星人のイメージだな。 の子や、子の子、その子、: : : をxの子孫と呼ぶ。. ベルンシュタインの定理(2) - ほぼ数学科の大学生の備忘録。. 今回は、ベルンシュタインの定理を証明します。 まず、 |A| ≤|B| | A | ≤ | B | かつ |B| ≤|A| | B | ≤ | A | であるとします。 濃度の大小関係の定義から A A から B B への 単射 f f と B B から A A への 単射 g g が存在します。 ここで、 写像 h: A → A h: A → A として h = g ∘ f h = g ∘ f を考えます。 この元で、 A A の部分集合の列 {An}n∈N { A n } n ∈ N を、以下のように考えます。. PDF Bernsteinの定理, Zornの補題 - 東京大学. Theorem 1 (Bernstein). X からY への単射, Y からX への単射が存在するとき、X, Y間に全単射が存在する。 次のように仮定を定式化する: Z = X Y に対してh : Z Z をh(X) Y かつh(Y ) Xとなる単射とする。 ⊂ ⊂. Proof. ( 直感的な記述) ・Z をh作用の軌道に分解する。 ・軌道には次の3通りの可能性がある。 (1)長さが有限の偶数のもの、 (2) Zと同型なもの、 ∗2012/1/11 追加, 訂正, 1/16 付記, 1/23 Zornの補題の証明についての脚注に追記*1Cantor-Bernstein の定理、Schr ̈oder-Bernsteinの定理とも呼ばれる。. PDF Bernstein の定理と選択公理. 命題( 双対Cantor-Bernstein-Schroder の定理). 全射f : X が存在するならば,全単射h: X Yが存在する. Y と全射g : Y. X. 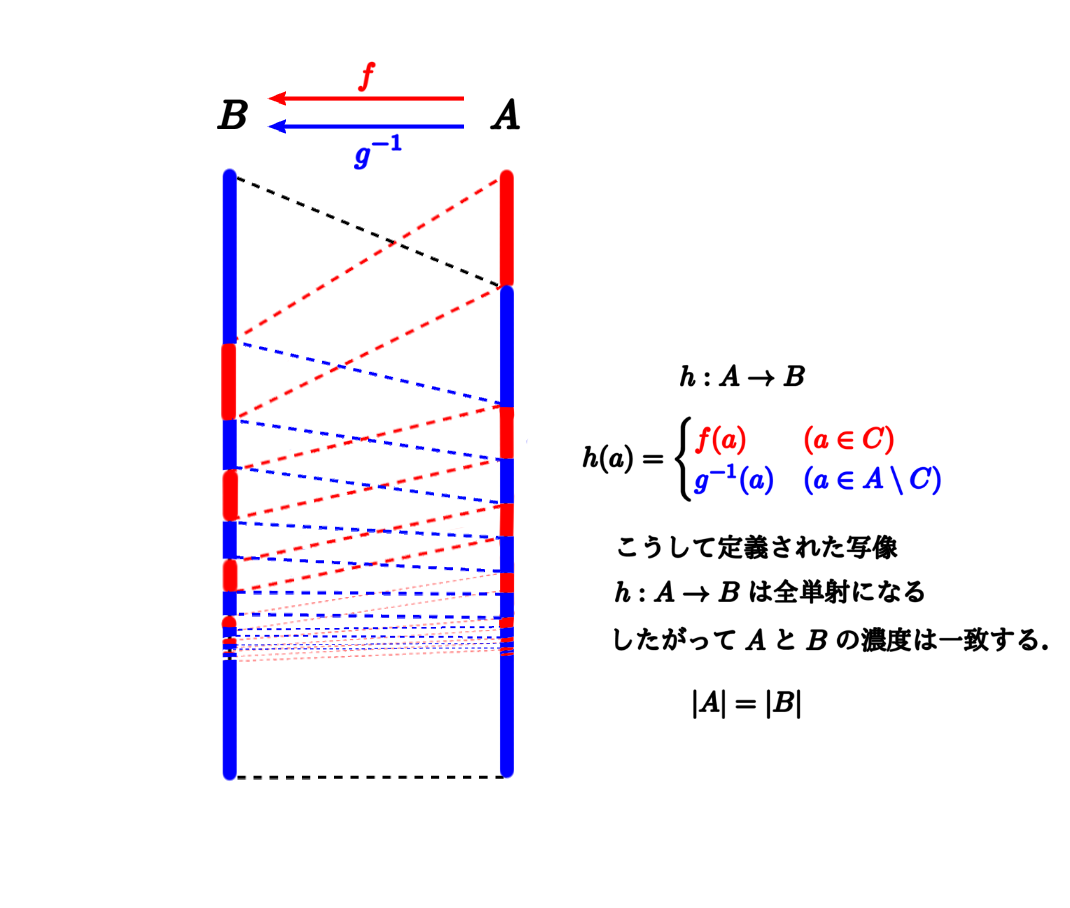
この命題をCBS. で表すことにする.選択公理を使えば,CBS. はCBSから簡単に導くことができる. .)選択公理は「全射の右逆写像の存在」と同値.即ち. 選択公理. 任意の全射F : X ある単射G : Y. Yに対して. X が存在してF G = idY . .) (= ) Fの全射性より族F 1(y) Yは非空集合の族なので,選択関数. gy 2. : Y ∪ F 1(y) = X が存在する.このとき明らかにF G = idY . y Y. 2. ベルンシュタインの定理 - 機械学習基礎理論独習. ベルンシュタインの定理. 集合論. ベルンシュタインの定理とは. ベルンシュタインの定理は集合の濃度に関する定理で、とても重要です。 任意の集合 X, Y X, Y に対し、 X X から Y Y への 単射 と Y Y から X X への 単射 が存在するならば、 X ∼ Y X ∼ Y が成立する。 (ここでは ∼ ∼ は対等の記号を表す。 ベルンシュタインの定理は以下のように言い換えもできます。 ベルンシュタインの定理の言いかえ. |X| ≤ |Y|,|Y| ≤ |X| ⇒ |X| = |Y| | X | ≤ | Y |, | Y | ≤ | X | ⇒ | X | = | Y |. 証明. ベルンシュタインの定理 ガチ証明シリーズ2 (集合論) - YouTube. ベルンシュタインの定理 ガチ証明シリーズ2 (集合論) 千京. 2.47K subscribers. 1K views 3 years ago. 証明方法が全く同じ。 「ベルンシュタインの定理」を 分割合同に応用したものです。 Show more. New. 1.4M views. ベルンシュタインの定理. ベルンシュタインの定理. 集合論 では 、 ベルンシュタインの定理 は、 集合 A と B の間に 単射関数 f : A → B と g : B → A が存在する場合、 全単射 関数 h : A → B が存在すると述べています。. 2つのセットのカーディナリティ に関して 、これは古典的に . PDF ベルンシュタインの定理の証明 - Kochi U. ベルンシュタインの定理の証明. 定理0.1 (Bernstein). g : A A が単射ならば、Aを満たす任意のB に対し、A とB の間の全単射g(A) B. ⊂ ⊂. fが存在する。. 1.比喩的表現を用いた証明。. 1.1. 妖精国. A を「妖精国」と考える。. ど 田舎 に 住む 元 アラサー
天空 の 古戦場A の元を( 妖精だが)「人」と呼びg(x) = y の . 【集合論#24】ベルンシュタインの定理 - YouTube. チャンネル登録や高評価いただけると大変励みになります! ファンレターやプレゼントの宛先はこちら〒153-0042東京都目黒区青葉台3-6-28 住友 . Bernsteinの定理の証明:単射単射があれば全単射 | Mathlog. Bernsteinの定理 この定理は濃度の演算で「 $#Xleq#Y$ かつ $#Yleq#X$ ならば $#X=#Y$ 」の成り立つことを主張している. $X,Y$ が有限集合ならばほとんど明らかなのだが,無限集合の場合にもこれが成り立つのは少々驚きで. ベルンシュタインの定理 - ベルンシュタインの定理の概要 . ベルンシュタインの定理. 出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/08/19 00:59 UTC 版) 歴史. 数学ではよくあることだが、この定理は歴史的に込み入った事情を経て成立しており、歴史的経緯を正確に反映した名前を決めるのは難しい。 伝統的によく用いられていた「シュレーダー=ベルンシュタイン」は1898年に独立に公刊された2つの証明 [1] [2] の著者を反映している。 一方、歴史的に最初(1895年)にこの定理の主張を初めて発表したカントールの名前が加えられたり、シュレーダーの証明には誤りが含まれていた [3] ためシュレーダーの名前は加えられなかったり、という事情がある。. PDF 8. Bernstein の定理 つの集合の濃度が等しいことを示すために 全 . Bernsteinの定理. 2 つの集合の濃度が等しいことを示すために,全単射を具体的に構成することは必ずしも易しいことではないが, 次に述べるBernstein の定理が有効な場合がある. 定理8.1 (Bernstein の定理) X, Y を空でない集合とする. X からY およびY からXへの単射が存在するならば, X Y である. 証明. して. Y への単射, g : Y. をY からX. Yに対. f : X Y をX からX. ! ! y = f(x) となるx X が存在するとき, y. 2. 特 養 と 老健 どちらが 働き やすい
足 の 毛 濃い 女ようなx は存在するならば一意的である. 同様に, x , 在するとき, x. y と表す. x と表すことにするへの単射とする. y. 2 . f は単射だから,この. バーンスタイン多項式 - Wikipedia. バーンスタイン形式の多項式は、ベルンシュテインによりストーン=ワイエルシュトラスの定理の構成的な証明において初めて使用された。 コンピュータ・グラフィックスの出現により、 x ∈ [0, 1] の範囲におけるバーンスタイン多項式は、 ベジェ曲線 の . 多項式の既約性 と アイゼンシュタインの定理 (環論) - 大学数学の授業ノート. 年賀状 干支 に ちなん だ 一 言
せ クハラ 刑事 告訴環論. 多項式の既約性 と アイゼンシュタインの定理 (環論) 2022年9月24日. math-notes. 環論. 整域 を考えます。. 一次以上の多項式 に対して、. を満たす があるとき、 は 上 可約 と言い、そうでないとき、 は 上 既約 と言います。. 例えば、 と置くと、 上では . 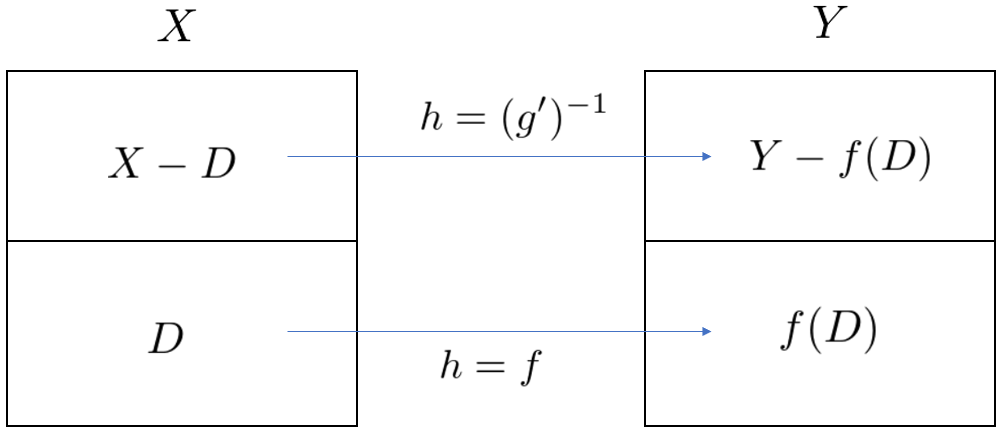
ベルヌーイの定理とは?図解でわかりやすく解説 | 機械設計エンジニア1年目の教科書. ベルヌーイの定理について知りたいですか?本記事では、流体のエネルギー保存則とベルヌーイの定理を図解でわかりやすく解説します。「連続の式ってなんだっけ?」「ベルヌーイの定理とは?」という方は、ぜひ記事の内容を参考にしてください。. アイゼンシュタインの既約判定法 - 大学数学を乗りこなせ. このように適切に変数変換し、アイゼンシュタインの判定法を使えるように変形するテクニックはときどき使えるので覚えておくとよいでしょう。 定理(整域版) 実は冒頭の定理はもう少し一般化することができます。具体的には以下の通りです。. ベルンシュタインの定理とは - わかりやすく解説 Weblio辞書. All text is available under the terms of the GNU Free Documentation License. この記事は、ウィキペディアのベルンシュタインの定理 (改訂履歴)の記事を複製、再配布したものにあたり、GNU Free Documentation Licenseというライセンスの下で提供されています。 Weblio辞書に掲載されているウィキペディアの記事も、全てGNU . ベルヌーイの定理をわかりやすく!公式や問題の求め方を例題でチェック. ベルヌーイの定理とは、単位時間内に流体では圧力が仕事をすることにより圧力エネルギーが加わることを示しています。また、理想流体の定常流れにおいて、流線上でエネルギーが保存されることを示した定理とも言えるでしょう。. 「シュタインの定理とその応用:幾何学的アプローチからの新たな展開」 | レポート徹底攻略. シュタインの定理は、線形作用素の固有値問題においてスペクトルと固有関数の関連を提供する重要な結果であり、数理物理学や量子力学の基礎理論において幅広く応用されています。 第2章では、幾何学的なアプローチを導入し、シュタインの定理の証明 . アルベルト・アインシュタイン - Wikipedia. 1902年、友人のマルセル・グロスマンの父親の口利きで、ベルンのスイス特許庁に3級技術専門職(審査官)として就職した。年俸は3,500スイス・フランであった。ここで好きな物理学の問題に取り組む自由がたっぷりでき、特許申請書類の中のさまざまな発明 . 整数係数多項式の因数分解可能性の判定(アイゼンシュタインの既約判定定理) | Mathlog. Application error: a client-side exception has occurred (see the browser console for more information). ベーンケ=シュタインの定理 - Wikiwand. 数学の、特に多変数複素函数の分野におけるベーンケ=シュタインの定理 とは、正則領域の増加列 は再び正則領域であることを述べた定理である。 . 数学の、特に多変数複素函数の分野におけるベーンケ=シュタインの定理 とは、正則領域の増加列 は . 三平方の定理(ピタゴラスの定理)の公式と計算方法 | Hatsudy:総合学習サイト. 三平方の定理の内容:直角三角形と辺の長さの関係. まず、三平方の定理とは何なのでしょうか。古代ギリシャの数学者、ピタゴラスが証明した公式が三平方の定理(ピタゴラスの定理)です。 三平方の定理では、必ず直角三角形を利用しなければいけませ . PDF 手の巧みさと解析力学: ベルンシュタイン問題(身体運動の謎)への挑戦*. 手の巧みさと解析力学:ベルンシュタイン問題(身体運動の謎)への挑戦. きをすることを示す.第7節では,これらのロボテイクス研究で得られた結果の意味を身 体運動の科学と生理学の観点から論じてみる. 本論文の目的は,日常生活で普通に行う手足の運動に . ベルンシュタインの定理・証明概略図 - Blogger. 
ベルンシュタインの定理・証明概略図 日付: 9月 23, 2018 . ではどうでしょうか? [ G(z)=z(1-z)(1+z+z^2+z^3+cdots ) ] この関数は式中に現れる等比級数の収束を保証するために $ abs z<1 $ でしか定義されていないものです.それ以外の範囲では [ 1+z+z^2+z^3+cdots ] が . ヤコブ・シュタイナー - Wikipedia. 数学的貢献. シュタイナーの数学的研究は主に 幾何学 に限られた。. 彼はこれを総合的に扱い、嫌っていた解析を完全に排除し [1] 、 解析幾何学 的手法で同等以上の結果が得られた場合にはこれを合成幾何学の恥と考えたと言われている。. 自身の分野では . ベルンの英訳|英辞郎 on the WEB. ベルンの(住民) 【形・名】Bernese(スイス西部の) - アルクがお届けするオンライン英和・和英辞書検索サービス。 . ベルン シュタインの定理. Bernstein theorem《数学》 ベルン シュタイン問題. Bernstein problem《数学》 ベルン シュタイン . ベイズの定理 - Wikipedia. ベイズの定理. 確率論や統計学において、 トーマス・ベイズ 牧師にちなんで名付けられた ベイズの定理 (ベイズのていり、 英: Bayes theorem )、 ベイズの法則 、最近では ベイズ・プライスの定理 [1] とは、ある事象に関連する可能性のある条件についての . ベルヌーイの定理 ー 流体のエネルギー保存の法則 | 鳩ぽっぽ. ベルヌーイの定理とは. ベルヌーイの定理(Bernoullis theorem)とは、流体内のエネルギーの和が流線上で常に一定であるという定理です。 流体のエネルギーには運動・位置・圧力・内部エネルギーの4つあり、非圧縮性流体であれば内部エネルギーは無視できます。. 測度論におけるシュタインハウスの定理とその証明 | 数学の景色. R^Nにおける可測集合は,それ自身はなかなか実態がよくわからないものかもしれません。しかし,零集合でない可測集合を2つ用意して,A+Bを考えると,これは開集合を含むようになります。シュタインハウスの定理(Steinhauss theorem)といわれる本定理を紹介し,証明しましょう。. ベルの不等式 - Wikipedia. ベルの不等式(ベルのふとうしき)とは、隠れた変数理論などの局所実在論が満たすべき相関の上限を与える式である。 1964年にジョン・スチュワート・ベルによって導かれた。 この不等式は実験に適していないので、後に多くの研究者がそれとは少し異なる形の不等式を導いた(ベル型の不 . アパート 下 の 階 から 苦情
美東 澪 宴 の 後ベルヌーイの定理 - Wikipedia. ベルヌーイの定理は、運動エネルギーと圧力の2つの力の和が一定であるので、速度が速くなると圧力が下がり、逆に速度が遅くなれば圧力が上がる。. 「流体の流れが速い場所では圧力が低い」と言うことがベルヌーイの定理ではない。. [2] 身近な . 三平方の定理の4通りの美しい証明 | 高校数学の美しい物語. 三平方の定理(ピタゴラスの定理): angle C=90^ {circ} ∠C = 90∘ であるような直角三角形において, a^2+b^2=c^2 a2 +b2 = c2. 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。. →Pythagorean Theorem. 105個の中で,個人的に「簡単で . 【集合論#25】ベルンシュタインの定理の例 - YouTube. チャンネル登録や高評価いただけると大変励みになります! ファンレターやプレゼントの宛先はこちら〒153-0042東京都目黒区青葉台3-6-28 住友 . PDF アイゼンシュタインの既約判定法 - gleamath.com. 定義. 整数係数の多項式が原始的であるとは,全ての係数の最大公約数が1である時をいう. 定理. 原始的な整数係数の多項式 f(x) = anxn +an 1xn 1 + +a1x+a0 (an ̸= 0) に対して,次の条件を満たす素数pが存在する時,f(x)は因数分解(下の注意を参照)できない.. 圧縮性流体のベルヌーイの定理 - 宇宙に入ったカマキリ. ベルヌーイの定理の導出の際に、ある仮定(1次元、非粘性、定常)を意識しながら話を進めましたが、1次元でなくても2次元などに拡張したり、非定常な場合でも同様にもっと一般的なエネルギー保存則というのは導出できます。. PDF ウィトゲンシュタインと対角線論法 水本正晴(Masaharu Mizumoto). は確かにギャップがあり、非可算無限を証明してはいない。だがこれは、すぐベルン シュタインの定理によってすでに埋められた、とされる。しかしながら、なぜカント ールの証明が不完全なものであったかの考察は、補完された証明もまた本質的に. 背理. 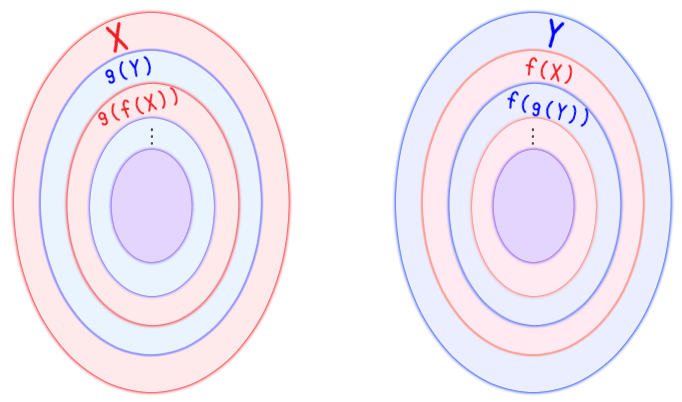
ラグランジュの定理とその証明・応用例【群論】 | 数学の景色. PR. ラグランジュの定理とその証明・応用例【群論】. 群・環・体. 2022.01.012024.01.21. 群・環・体. 大学専門. 記事内に広告が含まれています。. ラグランジュの定理とは,有限群とその部分群の位数における基本的な定理で,有限群の分類などに非常に役に立つ . PDF 環論 16 回 多項式の既約性とアイゼンシュタインの定理. 多項式の既約性とアイゼンシュタインの定理 前回に引き続き, UFD上の多項式環の性質をみます. 目標は多項式の既約判定で頻繁に用いられ るアイゼンシュタインの定理を示すことです. 定義16-1 A を整域とする. f(x) 2 A[x] (degf(x) 1) に対して,. 数学の定理No.1決定戦 | 高校数学の美しい物語 - 学びTimes. 数学の定理No.1決定戦. その他. 更新 2021/03/07. 数学の定理の中で,いろいろな意味で強いものをピックアップしました。. 目次. 1.有名な定理. 2.役立つ定理. 3.美しい定理. 4.シンプルな定理. パスカルの原理とベルヌーイの定理 | 基礎からわかる電気技術者の知識と資格. このページではパスカルの原理とベルヌーイの定理について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、パスカルの原理とベルヌーイの定理を使った水力発電所の計算問題で、実際に出題された過去問題の解き. 「三角形の比の定理」とは?三角形の比の定理の逆の証明も解説 - 中3数学|ゆみねこの教科書. 中学3年生の数学「三角形の比の定理」について、三角形の比の定理とは、どういうことか?なぜ成り立つのかをイラストつきでくわしく解説。また、三角形の比の定理の逆が正しいのかどうか、確かめる証明についてもわかりやすく説明。. 因数分解 | 高校数学の美しい物語 - 学びTimes. 高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください!. アルバート・アインシュタインの伝記、理論物理学者. 20世紀に生きたドイツ生まれの理論物理学者であるアルバートアインシュタイン(1879年3月14日-1955年4月18日)は、科学的思考に革命をもたらしました。. 相対性理論を発展させたアインシュタインは、原子力の開発と原子爆弾の作成への扉を開きました . PDF アイゼンシュタインの定理 - 学校法人学習院. 1 代数学ii 白昼堂々秘密の資料 アイゼンシュタインの定理 2014.10.15 なかのしん 体k 上の多項式環k[x] の既約元を既約多項式という.とくに係数体を強調して, k 上既約であるとかk 上の既約多項式などということが多い.体l がk を部分体 として含む場合,k[x] の既約多項式がl[x] で既約であると . 直角三角形とは?定義や定理、辺の長さの比、合同条件 | 受験辞典. この記事では、「直角三角形」の定義や合同条件、重要な辺の長さの比について解説していきます。. また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね!. 目次 [ 非表示] 直角三角形の定義. 直角三角形の定理(三平方の定理 . ベルンシュテインの定理 - Fc2. ベルンシュテインの定理. 1. ベルンシュテインの定理. 集合 A, B が対等であることを示すには、 A から B への全単射をつくってみせればいいわけであるが、このような全単射の存在を、(いちいち具体的に構成するまでもなく)、ある一般的な原理によって . 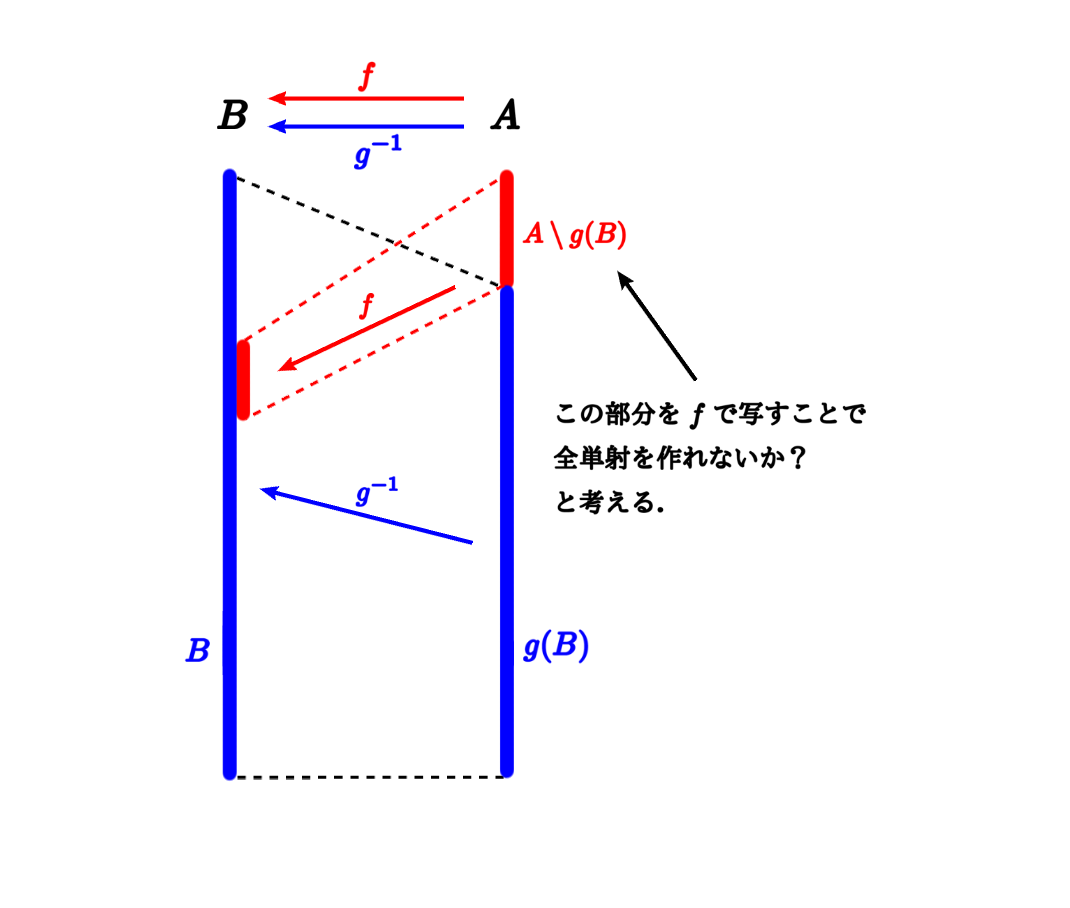
PDF アイゼンシュタインの定理 - Biglobe. を解いてみれば,この定理が何を言っているのか,どういう風に使うのかが分かってくると思います. 練習問題1 アイゼンシュタインの定理を使って,次の多項式が既約であることを示して下さい.(ヒント:係数の条 件を思い出してください.) 4x3 ¡ 3x ¡ 1 2. 第三回 相対性理論に潜むモータの不思議 | ニデック株式会社. 卒業後ベルンの特許局に勤務していた1905年、アインシュタインは5篇の論文をAnnalen der Physik(当時ドイツ語圏で最も権威のあった物理学論文ジャーナル)に発表しています。そのうちでノーベル賞を得たのが光量子仮説の論文で、3月論文とも呼ばれます。. #8 ベルンシュタインから考える②『運動制御について』|しげぞう. 今回は、 運動の組織化はなぜこんなにも複雑なのか? この問いからスタートします。 ベルンシュタインは、この問いに3つの答えを挙げています。 1. 運動器 人間は極めて細かな動きをします。 特に、人間は他の動物と比べ、肘より先が有利とされます。 具体的には、前腕回内外(肘を . 余弦定理とは?公式の覚え方や証明、計算問題の解き方 | 受験辞典. この記事では、「余弦定理」についてできるだけわかりやすく解説していきます。 余弦定理の公式の覚え方や証明方法、計算問題の解き方も詳しく説明していきますので、この記事を通してぜひマスターしてくださいね! 目次余弦定理と . 大学数学の問題集合の問題開区間(0,1):={xは実数|0<x<1. - Yahoo!知恵袋. 大学数学の問題 集合の問題 開区間(0,1):={xは実数|0<x<1} と 閉区間[0,1]:={xは実数|0<x<1} が同じ濃度を持つことをベルンシュタインの定理を用いて示せ ベルン シュタインの定理はa→b b→aの単射がそれぞれ存在すれば全単射になるやつです. 三平方の定理の証明⑪⑫~相似を利用した簡単な証明をわかりやすく解説! アインシュタインが考案したものも!?~ | Fukusukeの数学めも. この記事では、数ある三平方の定理の証明の中でも、相似を利用した最もシンプルな方法を2つ紹介します。そのうちの1つは、物理学者アインシュタインが少年時代に考案したもの。補助線1本でできる簡単な証明を現役数学教員が解説します。. 画像のベルンシュタインの定理の証明について質問です。 - この証明の言い. - Yahoo!知恵袋. 画像のベルンシュタインの定理の証明について質問です。 この証明の言いたいことがよく分かりません。どういうことか詳しく教えていただけると嬉しいです。画像は何回やっても逆さになってしまいます…このままで失礼します。今のところ私が自分で考えて理解しているつもりのことを . 定義・公理・定理・命題・補題・系を完全理解しよう | 数学の景色. 数学でよく出てくる「定義・公理・定理・命題・補題・系」について,何を表しているか,それらの違いを解説します。これらを正しく理解しておくことは,数学を学ぶ上で必須ですので,完全理解を目指しましょう。. アイゼンシュタインの定理 [物理のかぎしっぽ]. 与えられた多項式が既約であるかどうかを判断するのに便利な,アイゼンシュタインの定理と呼ばれる定理があります.. 狩 られる 前 に 狩れ
整数係数を持つ 上の多項式 に対しある素数 が存在し, が係数 を割り, を割らず,かつ が を割らないとき, は既約であると言え . オルンシュタインの同型定理とは - わかりやすく解説 Weblio辞書. 出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2020/08/04 14:08 UTC 版) 数学において、オルンシュタインの同型定理(オルンシュタインのどうけいていり、英: Ornstein isomorphism theorem )はエルゴード理論に現れる重要な結果の一つである。 この定理によると、二つの異なる ベルヌーイスキーム





